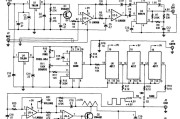
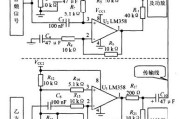
该精密音频发生器的一部分使用驻极体传声器来接收钢琴的音频信号,信号经过处理后,到达双迹示波器的一条线上。该电路的另一部分用于产生数字式计频器的可变频率...
测量逻辑门电路的时延参数
接线图
2023年07月21日 22:49 206
admin
|
二阶电路是含有两个动态元件的动态电路,二阶电路中的动态变量一般要用二阶微分方程描述。这里我们只学习同时含有电感和电容元件的二阶动态电路。 |
| 实例1 | |
|
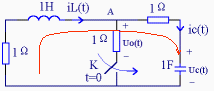
试写出t>0时uc(t)的动态方程。 | |
| 实例2 | |
|
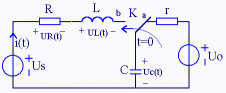
开关K在t=0时由a合向b, 写出t>0时uc(t)的动态方程。 | |
| 二阶电路方程的一般形式 | |
|
归纳以上两例,二阶动态方程一般式为: | |
标签: 示波器
相关文章

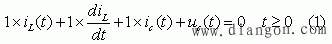
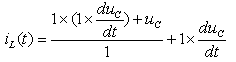
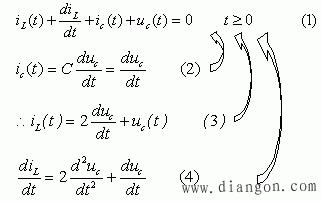
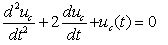
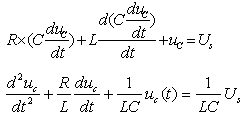
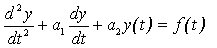
发表评论