交流发电机电压源是一台发电机,它从不同形式的能量产生电动势。最常见的电压源是交流发电机和电池。交流发电机通过机械旋转转换能量以产生交流信号,由于电...
电路替代定理
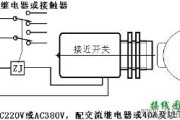
接线图
2023年07月21日 22:52 193
admin
一、叠加定理
叠加定理在线性电路的分析中起着重要的作用,它是分析线性电路的基础。线性电路中很多定理都与叠加定理有关。
 叠加定理(superposition principle):在线性电阻电路中,任一支路电流(或支路电压)都是电路中各个独立电源单独作用时,在该支路产生的电流(或电压)的叠加。
叠加定理(superposition principle):在线性电阻电路中,任一支路电流(或支路电压)都是电路中各个独立电源单独作用时,在该支路产生的电流(或电压)的叠加。
如图电路,计算U2 、I1 。
参考节点如图所示,对节点①列节点电压方程得:


每一部分的响应(response)均与对应的激励(excitation) 成线性关系。
令电压源和电流源单独作用,将各个激励下的响应叠加:

当一个电源单独作用时,其余电源不作用,就意味着取零值。即对电压源看作短路,而对电流源看作开路。即如下图:

通过回路电流法可得:线性电阻电路中任意支路的电压等于各电源(电压源、电流源)在此支路产生的电压的代数和。

支路电流是回路电流的线性组合,支路电流满足叠加定理。
同样可以证明:线性电阻电路中任意支路的电压等于各电源(电压源、电流源)在此支路产生的电压的代数和。
应用叠加定理要注意的问题
(1) 叠加定理只适用于线性电路(电路参数不随电压、电流的变化而改变)。
(2)叠加时只将独立电源分别考虑,电路的结构和参数(负载和受控源)不变。



例4. 利用叠加定理求电流I、电压U和2Ω电阻上消耗的功率。

二、齐次定理
当电路中只有一个激励(独立源)时,则响应(电压或电流)与激励成正比。

齐次定理只适用于线性电路,它描述了线性电路的比例特性。
例如:
显而易见:

若US增加 n 倍,各电流也会增加 n 倍。
2.应用:用齐次定理分析梯形电路特别有效
例5. 已知:RL= 2Ω,R1= 1Ω,R2= 1Ω,uS= 51V。
求电流 i 。

解:方法1:分压、分流。
方法2:电源变换。
方法3:用齐性原理(单位电流法)。

本例计算是先从梯形电路最远离电源的一段开始,倒退至激励处。这种计算方法称为“倒推法”。
3.可加性 (additivity property)分析

线性电路中,所有激励都增大(或减小)同样的倍数,则电路中响应也增大(或减小)同样的倍数。
例9. 如图电路,NS为有源网路,当US= 4V时,I3= 4A;当US= 6V时,I3= 5A;求当US= 2V时,I3为多少?

解:由叠加定理和线性定理,I3可表示为

叠加定理在线性电路的分析中起着重要的作用,它是分析线性电路的基础。线性电路中很多定理都与叠加定理有关。
 叠加定理(superposition principle):在线性电阻电路中,任一支路电流(或支路电压)都是电路中各个独立电源单独作用时,在该支路产生的电流(或电压)的叠加。
叠加定理(superposition principle):在线性电阻电路中,任一支路电流(或支路电压)都是电路中各个独立电源单独作用时,在该支路产生的电流(或电压)的叠加。 如图电路,计算U2 、I1 。
参考节点如图所示,对节点①列节点电压方程得:


每一部分的响应(response)均与对应的激励(excitation) 成线性关系。
令电压源和电流源单独作用,将各个激励下的响应叠加:

当一个电源单独作用时,其余电源不作用,就意味着取零值。即对电压源看作短路,而对电流源看作开路。即如下图:

通过回路电流法可得:线性电阻电路中任意支路的电压等于各电源(电压源、电流源)在此支路产生的电压的代数和。

支路电流是回路电流的线性组合,支路电流满足叠加定理。
同样可以证明:线性电阻电路中任意支路的电压等于各电源(电压源、电流源)在此支路产生的电压的代数和。
应用叠加定理要注意的问题
(1) 叠加定理只适用于线性电路(电路参数不随电压、电流的变化而改变)。
(2)叠加时只将独立电源分别考虑,电路的结构和参数(负载和受控源)不变。
暂时不予考虑的恒压源应予以短路,即令US=0;
暂时不予考虑的恒流源应予以开路,即令 IS=0。

(3)分电路中各支路电流、电压的参考方向要与原电路中的一致。原电路中各电压、电流的最后结果是各分电压、分电流的代数和。
(4) 叠加原理只能用于电压或电流的计算,不能用来求功率。如:

(5) 运用叠加定理时也可以把电源分组求解,每个分电路的电源个数可能不止一个。




例4. 利用叠加定理求电流I、电压U和2Ω电阻上消耗的功率。

二、齐次定理
1.定义
线性电路中,所有激励(独立源)都增大(或减小)同样的倍数,则电路中响应(电压或电流)也增大(或减小)同样的倍数。当电路中只有一个激励(独立源)时,则响应(电压或电流)与激励成正比。

齐次定理只适用于线性电路,它描述了线性电路的比例特性。
例如:
显而易见:

若US增加 n 倍,各电流也会增加 n 倍。
2.应用:用齐次定理分析梯形电路特别有效
例5. 已知:RL= 2Ω,R1= 1Ω,R2= 1Ω,uS= 51V。
求电流 i 。

解:方法1:分压、分流。
方法2:电源变换。
方法3:用齐性原理(单位电流法)。

本例计算是先从梯形电路最远离电源的一段开始,倒退至激励处。这种计算方法称为“倒推法”。
3.可加性 (additivity property)分析

线性电路中,所有激励都增大(或减小)同样的倍数,则电路中响应也增大(或减小)同样的倍数。
例9. 如图电路,NS为有源网路,当US= 4V时,I3= 4A;当US= 6V时,I3= 5A;求当US= 2V时,I3为多少?

解:由叠加定理和线性定理,I3可表示为

标签: 电源
相关文章

发表评论