组合逻辑电路中的竞争冒险
接线图
2023年07月21日 22:52 248
admin
组合逻辑电路的设计,通常以电路简单,器件最少为目标。用代数法和卡诺图法来简化逻辑函数,就是为了获得最简的形式,以便用最少的门电路来组成逻辑电路。在设计中普遍采用中、小规模集成电路(一片包括数个门至数十个门)产品,根据具体情况,尽可能减少所用的器件数目和种类,使组装好的电路结构紧凑,达到工作可靠、经济的目的。采用小规模集成器件设计组合逻辑电路的一般步骤如图1所示。
图1 组合逻辑电路设计步骤
首先将逻辑功能要求抽象成真值表的形式。由真值表可以很方便地写出逻辑函数的表达式。在采取小规模器件时,通常将函数化简成最简与-或表达式,使其包含的乘积项最少,且每个乘积项所包含的因子数也最少。最后根据所采取的器件的类型进行适当的函数表达式变换,如变换成与非-与非表达式、或非-或非表达式、与或非表达式及异或表达式等。
必须说明的是,有时由于输入变量的条件(如只有原变量输入,没有反变量输入)或采取器件的条件(如在一块集成器件中包含多个基本门)等因素,采用最简与或式实现电路,不一定是最佳电路结构。下面通过一些例题说明采取小规模集成逻辑器件设计组合逻辑电路的基本方法。
例1 试用2输入与非门和反相器设计一个3输入(I0、I1、I2)、3输出(L0、L1、L2)的信号排队电路。它的功能是:当输入I0为1时,无论I1和I2为1还是0,输出L0为1,L1和L2为0;当I0为0且I1为1,无 论I2为1还是0,输出L1为1,其余两个输出为0;当I2为1且I0和I1均为0时,输出L2为1,其余两个输出为0。如I0、I1、I2均为0,则L0、L1、L2也均为0。
解:(1) 根据题意列出真值表,如表1所示
必须说明的是,有时由于输入变量的条件(如只有原变量输入,没有反变量输入)或采取器件的条件(如在一块集成器件中包含多个基本门)等因素,采用最简与或式实现电路,不一定是最佳电路结构。下面通过一些例题说明采取小规模集成逻辑器件设计组合逻辑电路的基本方法。
例1 试用2输入与非门和反相器设计一个3输入(I0、I1、I2)、3输出(L0、L1、L2)的信号排队电路。它的功能是:当输入I0为1时,无论I1和I2为1还是0,输出L0为1,L1和L2为0;当I0为0且I1为1,无 论I2为1还是0,输出L1为1,其余两个输出为0;当I2为1且I0和I1均为0时,输出L2为1,其余两个输出为0。如I0、I1、I2均为0,则L0、L1、L2也均为0。
解:(1) 根据题意列出真值表,如表1所示
表1 例1的真值表
输入 | 输出 |
I1 I2 I3 | L0 L1 L2 |
0 0 0 | 0 0 0 |
1 0 0 | 1 0 0 |
1 0 1 | 1 0 0 |
1 1 0 | 1 0 0 |
1 1 1 | 1 0 0 |
0 1 0 | 0 1 0 |
0 1 1 | 0 1 0 |
0 0 1 | 0 0 1 |
| (2) 根据真值表写出各输出表达式 | (3)根据要求将输出表达式变换为与非形式,并由此画出逻辑图 |
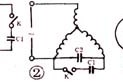
 |  图2 逻辑图 |
由此可画出逻辑图,如图2所示。该逻辑电路可用一片内含四个2输入端的与非门和另一片内含六个反相器的集成电路组成;也可用两片内含四个2输入端与非门的集成电路组成。原逻辑表达式虽然是最简形式,但它需一片反相器和一片3输入端的与门才能实现,器材数和种类都不能节省。由此可见,最简的逻辑表达式用一定规格的集成器件实现时,其电路结构不一定是最简单和最经济的。设计逻辑电路时应以集成器件为基本单元,而不应以单个门为单元,这是工程设计与理论分析的不同之处。
该电路可选取四2输入与非门74LS00和六反相器74LS04构成,也可以用两片74LS00。
例2 试设计一可逆的4位码变换器。在控制信号C=1时,它将8421码转换为格雷码;C=0时,它将格雷码转换为8421码。
解:(1)列出真值表,如表2所示。当C=1时,输入X3X2X1X0作为8421码,对应的输出g3g2g1g0为格雷码;当C=0时,输入则作为格雷码,对应的输出b3b2b1b0为8421码。此时,X3X2X1X0作为格雷码的排列顺序体现在它与b3b2b1b0的一一对应关系。

该电路可选取四2输入与非门74LS00和六反相器74LS04构成,也可以用两片74LS00。
例2 试设计一可逆的4位码变换器。在控制信号C=1时,它将8421码转换为格雷码;C=0时,它将格雷码转换为8421码。
解:(1)列出真值表,如表2所示。当C=1时,输入X3X2X1X0作为8421码,对应的输出g3g2g1g0为格雷码;当C=0时,输入则作为格雷码,对应的输出b3b2b1b0为8421码。此时,X3X2X1X0作为格雷码的排列顺序体现在它与b3b2b1b0的一一对应关系。

表2 例2中码变换关系真值表
(2)分别画出C=1和C=0时各输出函数的卡诺图,如图3(a)所示。
|
(3)由卡诺图可求得各输出逻辑表达式。若同时考虑C变量,当C=1时,有
| g3=X3C g2=(X3X2+X3X2)C=(X3⊕X2)C g1=(X2X1+X2X1)C=(X2⊕X1)C g0=(X1X0+X1X0)C=(X1⊕X0)C |
当C=0时,有
 |
由各输出逻辑表达式可得总的输出逻辑表达式
 |
由总的输出逻辑表达式可画出如图3(b)所示的逻辑图。

图3 例2的卡诺图和逻辑图 (b)逻辑图
从以上逻辑表达式和逻辑图可以看出,用异或门代替与门和或门能使逻辑电路比较简单。在化简和变换逻辑表达式时,应尽可能使某些输出作为另一些输出的条件,例如,利用Y2作为Y1的一个简单输入,Y1又作为Y0的一个输入,这样可以使电路更简单。在化简时,若注意综合考虑,使式中的相同项尽可能多,则可以使电路得到简化。此外,我们还将与或换成与非形式,从而减少了门电路的种类。该逻辑电路可由两片各含四2输入与非门(74LS00)和一片内含四个异或门(74LS86)的集成电路组成。
相关文章



发表评论