多级放大电路中引入某种负反馈组态可以改善它的许多性能指标,但不合适的反馈深度和多级放大电路的附加相移将可能使放大电路产生自激振荡,产生自激振荡的原因分析、判断方法、提出校正措施。
1、产生自激振荡的原因及条件
A ˙ f = A ˙ 1+ A ˙ F ˙ → 1+ A ˙ F ˙ =0→ A ˙ F ˙ =−1 → X ˙ i =0, X ˙ o ≠0 负反馈变性为正反馈。
{ | A ˙ F ˙ |=1 幅度条件 arg A ˙ F ˙ =±(2n+1)π(n为整数)相位条件
相位条件中有个附加相移 ± 180 o 。
以上两个条件都具备时,放大电路就将产生自激振荡。电路一旦自激,就意味着失去控制,不再能够实现正常放大工作。
产生自激振荡的原因分析:
我们在电路中引入的负反馈,实际上都是基于在中频区进行的。但 A ˙ 、 F ˙ 是频率的函数,由放大电路频率特性知道,在高频区或低频区, A ˙ 除了幅度下降,还有附加相移。这将可能导致 1+ A ˙ F ˙ =0,从而产生了自激振荡。
单级放大电路:附加相移 0~± 90 o ,不会自激。
两级放大电路:附加相移 0~± 180 o ,不会自激。
三级或三级以上放大电路:附加相移 0~± 270 o 以上,则肯定有个频率 f o ,将使附加相移 Δϕ= 180 o ,负反馈变性为正反馈。若这时 | A ˙ F ˙ | ≥1,则满足自激振荡条件,能够起振和振荡;若这时 | A ˙ F ˙ | <1,则不满足自激振荡条件,电路仍然是稳定的。
自激振荡频率来源:电路开机激励、外来干扰或者热噪声。
2、自激振荡的判断方法及稳定裕度
1.判断方法:
在自激振荡的两个条件中,相位条件是主要的,首先若相位条件满足了,即附加相移 ϕ A ˙ F ˙ = 180 o ,又满足 | A ˙ F ˙ | ≥1,放大器将产生自激。否则,不自激。
为此,我们用环路增益 A ˙ F ˙ 的频率特性—波特图来分析判断闭环放大电路的稳定性。
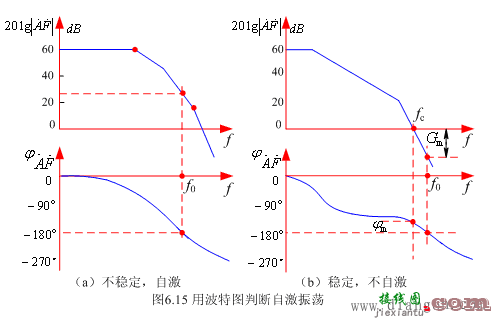
如图 6.15(a)和(b)所示分别表示不稳定与稳定的两种情况。
图6.15(a)中 f 0 处: arg A ˙ F ˙ = ϕ A ˙ F ˙ | f 0 =− 180 o ,对应的 20lg | A ˙ F ˙ | f 0 >0(即 | A ˙ F ˙ | >1)。
由此可见满足自激振荡条件,放大器不稳定,将产生自激。
图6.15(b)中 f 0 处: arg A ˙ F ˙ = ϕ A ˙ F ˙ | f 0 =− 180 o ,对应的 20lg | A ˙ F ˙ | f 0 <0(即 | A ˙ F ˙ | <1)。
由此可见不满足自激振荡条件,放大器稳定,不会产生自激。
2.稳定裕度:
引入负反馈后,为保证放大电路可靠工作,规定:
幅度裕度—— G m =20lg | A ˙ F ˙ | ϕ= 180 0 ≤-10 dB (对应 f 0 )
相位裕度—— ϕ m = 180 o + ϕ A ˙ F ˙ ( 20 lg | A ˙ F ˙ | = 0 ) ≥45o (对应 f c )
3、自激振荡的校正措施
若放大电路产生自激振荡,应适当采用措施破坏自激振荡的条件,以保证电路稳定工作。
方法1——减小反馈系数 | F ˙ | 。
改变反馈网络电阻值,减小反馈系数 | F ˙ | ,使当相位条件 ϕ A ˙ F ˙ | =− 180 o 时,对应的幅度条件 20lg | A ˙ F ˙ | f 0 <0。
方法简单,但反馈深度 | 1+ A ˙ F ˙ | ↓,不利于放大电路其他性能的改善。
方法2——接入 C 或 RC 校正,使主极点左移。
C 或 RC 接到某一级的输出端或者放大管的集电极、基极之间(密勒电容)(一般接到产生主极点 f HMIn 的那一级),在中、低频时, C 或 RC 基本不起作用。在高频时,使放大倍数快速下降, ϕ A ˙ F ˙ | = − 180 o 时,对应的 20lg | A ˙ F ˙ | f 0 <0。
实际工作中,常用一个小电容( PF 级)并在放大器的输出端试探,使高频段主极点左移。这种方法不影响反馈深度 | 1+ A ˙ F ˙ | 和放大电路其他性能,但将损失通频带。
例如,假设某三级放大电路的电压放大倍数为
A ˙ F ˙ = − 10 4 (1+j f 0.5 )(1+j f 1 )(1+j f 5 ) ×(−0.1)

主极点为 f H1 =0.5MHz ,通过接入 C 或 RC 校正,使主极点左移到 f ′ H1 ,从而使相位条件 ϕ A ˙ F ˙ | = − 180 o 时,对应的幅度条件 20lg | A ˙ F ˙ | f 0 <0。
两种消除自激振荡方法对应的 A ˙ F ˙ 波特图(示意图)如图6.16所示。





发表评论