实现模2除法的线路 循环校验码的核心逻辑线路是实现模2除的线路。按照前面介绍的方法,可将模2除的步骤分解归纳为两种操作:如果被除数或者余数最高位的值为
0,直接将余数左移一位;如果被除数或部分余数最高位的值为
1,用生成多项式G(x)作模2减,然后余数左移一位。

图2.2 实现模2除的逻辑图 对前述用G(x)=1011产生(7,4)校验码的例子,可采用图2.2所示线路,产生3位的余数。图中的模2减用异或门实现,左移一位由移位寄存器实现;用异或门的输出
控制左边一位寄存器的D
输入端,可同时实现模2减和左移。用最左一位的取值控制是否做模2减,当其为1时,减去的数就是生成多项式G(x)=1011。这里,被除数D是逐位串行送到移位寄存器的,且由CP脉冲同步。


图2.3 实现G(x)=1011的线性(7,4)分组码模2除线路图 由于G(x)固定不变,故G2可省去;只求三位余数,故G3和T0也失去意义。图2.2可简化为图2.3(a)。
对图2.3(a)的线路来说,在发送端,输入信息码D为1100,串行从低位送入,先左移三位形成1100000,再通过7步模2除,可在移位寄存器 T
3 T
2 T
1 中得到余数010;在接收端,对7位的CRC码字1100010,执行7步模2除之后,若在 T
3 T
2 T
1 得到000,表明CRC码字中无任何一位出错;若余数不为全0,可根据表2.4确定出错位置。
设T
i为T3T2T1某触发器当前状态,T
i'为次态,可用次态方程表示图2.3(a)的模2除
电路: T
3'=T
2, T
2'=T
3⊕T
1 , T
1'=T
3⊕D。
分别用被除数1100000和1010000验证取得余数为010和011的工作过程,见表2.6。读者可用模2除竖式计算各步结果并与之比较。
表2.6 图2.3(a)线路工作过程举例
步骤版权与免责声明 本网转载并注明自其它出处的作品,目的在于传递更多信息,并不代表本网赞同其观点或证实其内容的真实性,不承担此类作品侵权行为的直接责任及连带责任。其他媒体、网站或个人从本网转载时,必须保留本网注明的作品出处,并自负版权等法律责任。
如涉及作品内容、版权等问题,请在作品发表之日起一周内与本网联系,否则视为放弃相关权利。
标签:
线路码
相关文章
-
线路码型实验

实验 线路码型实验 一 实验目的1 了解线路码型概念2 了解CMI码的编解码原理3 初步建立系统的概念 二 实验原理及框图 我国邮电部从管理的...
2023-01-27
310
线路码
详细阅读
-
专用线路介绍,专用线路协议-HDLC
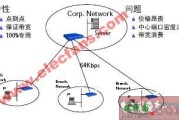
专用线路介绍 专用线路是透明的物理传输信道,由于它使用简便、覆盖面广,被广泛应用于企业网互联、专线 Internet 接入等。专用线路的明显缺陷是:...
2023-01-27
257
线路码
详细阅读
|



发表评论