图(a 为反相加法电路，其输入输出关系为： Vo=-(Vil+Vi2 当需要同相加法时，可采用图(b 所示电路，其输入输出关系为： Vo=Vil...
反相加法器原理图与电路图
接线图
2023年02月15日 18:11 299
admin
一、什么是加法器
加法器是为了实现加法的。
即是产生数的和的装置。加数和被加数为输入，和数与进位为输出的装置为半加器。若加数、被加数与低位的进位数为输入，而和数与进位为输出则为全加器。常用作计算机算术逻辑部件，执行逻辑操作、移位与指令调用。
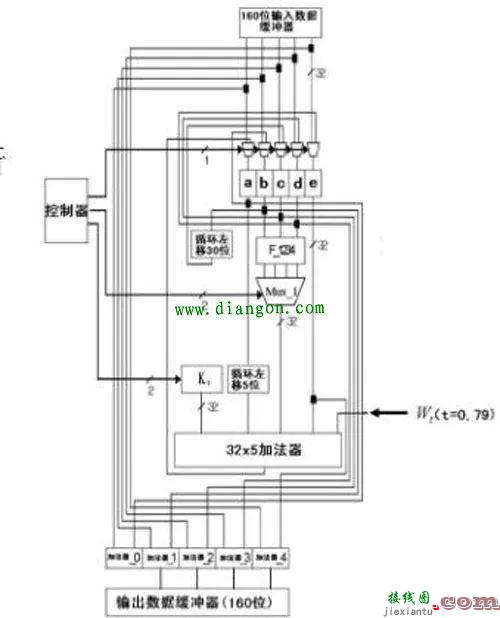对于1位的二进制加法，相关的有五个的量：1，被加数A，2，被加数B，3，前一位的进位CIN，4，此位二数相加的和S，5，此位二数相加产生的进位COUT。前三个量为输入量，后两个量为输出量，五个量均为1位。
对于32位的二进制加法，相关的也有五个量：1，被加数A(32位)，2，被加数B(32位)，3，前一位的进位CIN(1位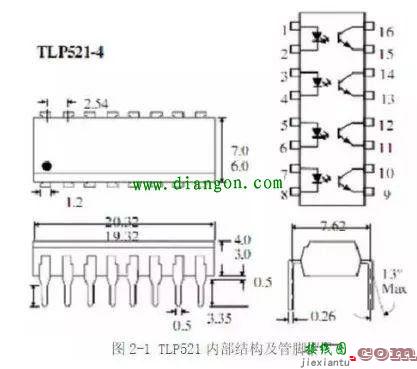
4，此位二数相加的和S(32位)，5，此位二数相加产生的进位COUT(1位)。
要实现32位的二进制加法，一种自然的想法就是将1位的二进制加法重复32次(即逐位进位加法器)。这样做无疑是可行且易行的，但由于每一位的CIN都是由前一位的COUT提供的，所以第2位必须在第1位计算出结果后，才能开始计算;第3位必须在第2位计算出结果后，才能开始计算，等等。而最后的第32位必须在前31位全部计算出结果后，才能开始计算。这样的方法，使得实现32位的二进制加法所需的时间是实现1位的二进制加法的时间的32倍。
基本方法
可以看出，上法是将32位的加法1位1位串行进行的，要缩短进行的时间，就应设法使上叙进行过程并行化。
类型
以单位元的加法器来说，有两种基本的类型：半加器和全加器。
半加器有两个输入和两个输出，输入可以标识为 A、B 或 X、Y，输出通常标识为合 S 和进制 C。A 和 B 经 XOR 运算后即为 S，经 AND 运算后即为 C。
全加器引入了进制值的输入，以计算较大的数。为区分全加器的两个进制线，在输入端的记作 Ci 或 Cin，在输出端的则记作 Co 或 Cout。半加器简写为 H.A.，全加器简写为 F.A.。
半加器：半加器的电路图半加器有两个二进制的输入，其将输入的值相加，并输出结果到和(Sum)和进制(Carry)。半加器虽能产生进制值，但半加器本身并不能处理进制值。
全加器：全加器三个二进制的输入，其中一个是进制值的输入，所以全加器可以处理进制值。全加器可以用两个半加器组合而成。
注意，进制输出端的最末个 OR闸，也可用 XOR闸来代替，且无需更改其余的部分。因为 OR 闸和 XOR 闸只有当输入皆为 1 时才有差别，而这个可能性已不存在。
二、加法器原理
设一个n位的加法器的第i位输入为ai、bi、ci，输出si和ci+1，其中ci是低位来的进位，ci+1(i=n-1，n-2，…，1，0)是向高位的进位，c0是整个加法器的进位输入，而cn是整个加法器的进位输出。则和
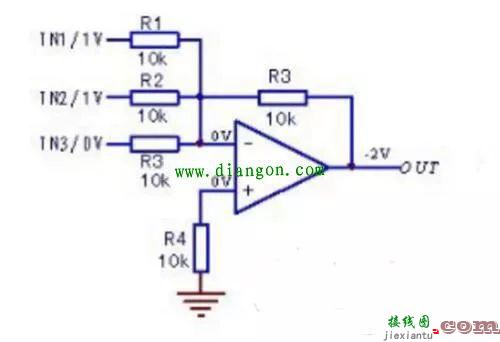si=aiii+ibii+iici+aibici ，(1)进位ci+1=aibi+aici+bici ，(2)
令 gi=aibi， (3)
pi=ai+bi， (4)
则 ci+1= gi+pici， (5)
只要aibi=1，就会产生向i+1位的进位，称g为进位产生函数;同样，只要ai+bi=1，就会把ci传递到i+1位，所以称p为进位传递函数。把式(5)展开，得到：ci+1= gi+ pigi-1+pipi-1gi-2+…+ pipi-1…p1g0+ pipi-1…p0c0(6) 。
随着位数的增加式(6)会加长，但总保持三个逻辑级的深度，因此形成进位的延迟是与位数无关的常数。一旦进位(c1~cn-1)算出以后，和也就可由式(1)得出。
使用上述公式来并行产生所有进位的加法器就是超前进位加法器。产生gi和pi需要一级门延迟，ci 需要两级，si需要两级，总共需要五级门延迟。与串联加法器(一般要2n级门延迟)相比，(特别是n比较大的时候)超前进位加法器的延迟时间大大缩短了。
三、反相加法器等效原理图
反相加法器电路，又称为反相求和电路，是指一路以上输入信号进入反相输入端，输出结果为多路信号相加之绝对值(电压极性相反)。如图中的a电路，当R1=R2=R3=R4时，其输出电压=IN1+IN2+IN3的绝对值，即构成反相加法器电路。当R4》R1时，电路兼有信号放大作用。
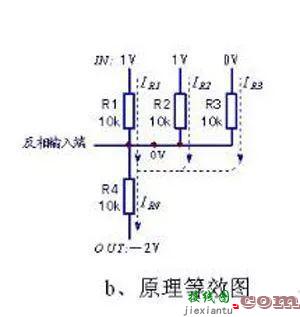
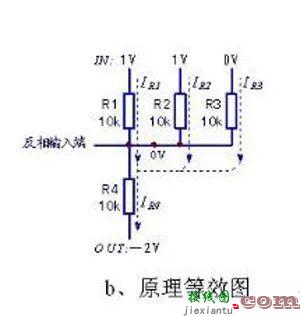图 反相加法器和原理等效图
反相加法器的基本电路结构为反相放大器，由其“虚地”特性可知，两输入端俱为0V地电位。这就决定了电路的控制目的，是使反相输入端电位为0V(同相输入端目标值为0V)。以上图a电路电路参数和输入信号值为例进行分析，则可得出如上图b所示的等效图。反相加法器的偏置电路总体上仍为串联分压的电路形式，但输入回路中又涉及了电阻并联分流的电路原理，可列等式：IR4=IR1+IR2+IR3。反相加法器的“机密”由此得以披露。
由于反相输入端为地电位0V，因而当输入信号IN3=0V时该支路无信号电流产生，相当于没有信号输入，由此变为IN1+IN2=-OUT。当IR1(1V/10k)=0.1mA，IR2(1V/10k)=0.1mA，此时只有当OUT输出为-2V时，才满足IR4=IR1+IR2的条件。
若将原理等效图进一步化简(见图中的c电路)，一个非常熟悉的身影便会映入我们的脑海：这不就是反相放大器电路吗?是的，没错，反相求和(反相加法器)电路，就是反相(含放大和衰减)器啊。
实际应用中，因同相加法器存在明显缺陷，因输入阻抗极高，信号输入电流只能经多个IN端自成回路(会造成输入信号电压相互牵涉而变化导致较大的运算误差)，除非各种IN信号源内阻非常小，才不会影响计算精度。因而应用较少。反相求和电路因其“虚地”特性，输入阻抗极低，使各路信号输入电流以“汇流模式”进入输入端，不会造成各输入信号之间的电流流动，故能保障运算精度，应用较多。
四、反相加法器电路与原理(图)
加法器是为了实现加法的。
即是产生数的和的装置。加数和被加数为输入，和数与进位为输出的装置为半加器。若加数、被加数与低位的进位数为输入，而和数与进位为输出则为全加器。常用作计算机算术逻辑部件，执行逻辑操作、移位与指令调用。
对于1位的二进制加法，相关的有五个的量：1，被加数A，2，被加数B，3，前一位的进位CIN，4，此位二数相加的和S，5，此位二数相加产生的进位COUT。前三个量为输入量，后两个量为输出量，五个量均为1位。对于32位的二进制加法，相关的也有五个量：1，被加数A(32位)，2，被加数B(32位)，3，前一位的进位CIN(1位
4，此位二数相加的和S(32位)，5，此位二数相加产生的进位COUT(1位)。要实现32位的二进制加法，一种自然的想法就是将1位的二进制加法重复32次(即逐位进位加法器)。这样做无疑是可行且易行的，但由于每一位的CIN都是由前一位的COUT提供的，所以第2位必须在第1位计算出结果后，才能开始计算;第3位必须在第2位计算出结果后，才能开始计算，等等。而最后的第32位必须在前31位全部计算出结果后，才能开始计算。这样的方法，使得实现32位的二进制加法所需的时间是实现1位的二进制加法的时间的32倍。
基本方法
可以看出，上法是将32位的加法1位1位串行进行的，要缩短进行的时间，就应设法使上叙进行过程并行化。
类型
以单位元的加法器来说，有两种基本的类型：半加器和全加器。半加器有两个输入和两个输出，输入可以标识为 A、B 或 X、Y，输出通常标识为合 S 和进制 C。A 和 B 经 XOR 运算后即为 S，经 AND 运算后即为 C。
全加器引入了进制值的输入，以计算较大的数。为区分全加器的两个进制线，在输入端的记作 Ci 或 Cin，在输出端的则记作 Co 或 Cout。半加器简写为 H.A.，全加器简写为 F.A.。
半加器：半加器的电路图半加器有两个二进制的输入，其将输入的值相加，并输出结果到和(Sum)和进制(Carry)。半加器虽能产生进制值，但半加器本身并不能处理进制值。
全加器：全加器三个二进制的输入，其中一个是进制值的输入，所以全加器可以处理进制值。全加器可以用两个半加器组合而成。
注意，进制输出端的最末个 OR闸，也可用 XOR闸来代替，且无需更改其余的部分。因为 OR 闸和 XOR 闸只有当输入皆为 1 时才有差别，而这个可能性已不存在。
二、加法器原理
设一个n位的加法器的第i位输入为ai、bi、ci，输出si和ci+1，其中ci是低位来的进位，ci+1(i=n-1，n-2，…，1，0)是向高位的进位，c0是整个加法器的进位输入，而cn是整个加法器的进位输出。则和
si=aiii+ibii+iici+aibici ，(1)进位ci+1=aibi+aici+bici ，(2)令 gi=aibi， (3)
pi=ai+bi， (4)
则 ci+1= gi+pici， (5)
只要aibi=1，就会产生向i+1位的进位，称g为进位产生函数;同样，只要ai+bi=1，就会把ci传递到i+1位，所以称p为进位传递函数。把式(5)展开，得到：ci+1= gi+ pigi-1+pipi-1gi-2+…+ pipi-1…p1g0+ pipi-1…p0c0(6) 。
随着位数的增加式(6)会加长，但总保持三个逻辑级的深度，因此形成进位的延迟是与位数无关的常数。一旦进位(c1~cn-1)算出以后，和也就可由式(1)得出。
使用上述公式来并行产生所有进位的加法器就是超前进位加法器。产生gi和pi需要一级门延迟，ci 需要两级，si需要两级，总共需要五级门延迟。与串联加法器(一般要2n级门延迟)相比，(特别是n比较大的时候)超前进位加法器的延迟时间大大缩短了。
三、反相加法器等效原理图
反相加法器电路，又称为反相求和电路，是指一路以上输入信号进入反相输入端，输出结果为多路信号相加之绝对值(电压极性相反)。如图中的a电路，当R1=R2=R3=R4时，其输出电压=IN1+IN2+IN3的绝对值，即构成反相加法器电路。当R4》R1时，电路兼有信号放大作用。
图 反相加法器和原理等效图反相加法器的基本电路结构为反相放大器，由其“虚地”特性可知，两输入端俱为0V地电位。这就决定了电路的控制目的，是使反相输入端电位为0V(同相输入端目标值为0V)。以上图a电路电路参数和输入信号值为例进行分析，则可得出如上图b所示的等效图。反相加法器的偏置电路总体上仍为串联分压的电路形式，但输入回路中又涉及了电阻并联分流的电路原理，可列等式：IR4=IR1+IR2+IR3。反相加法器的“机密”由此得以披露。
由于反相输入端为地电位0V，因而当输入信号IN3=0V时该支路无信号电流产生，相当于没有信号输入，由此变为IN1+IN2=-OUT。当IR1(1V/10k)=0.1mA，IR2(1V/10k)=0.1mA，此时只有当OUT输出为-2V时，才满足IR4=IR1+IR2的条件。
若将原理等效图进一步化简(见图中的c电路)，一个非常熟悉的身影便会映入我们的脑海：这不就是反相放大器电路吗?是的，没错，反相求和(反相加法器)电路，就是反相(含放大和衰减)器啊。
实际应用中，因同相加法器存在明显缺陷，因输入阻抗极高，信号输入电流只能经多个IN端自成回路(会造成输入信号电压相互牵涉而变化导致较大的运算误差)，除非各种IN信号源内阻非常小，才不会影响计算精度。因而应用较少。反相求和电路因其“虚地”特性，输入阻抗极低，使各路信号输入电流以“汇流模式”进入输入端，不会造成各输入信号之间的电流流动，故能保障运算精度，应用较多。
四、反相加法器电路与原理(图)
标签： 加法器
相关文章
发表评论