该步进脉冲发生器项目是步进控制器驱动的简单解决方案。它是一个非常重要的工具，可用于在独立模式下驱动步进器。它产生频率范围为 0-50Khz 的方波...
了解三运放仪表放大器
接线图
2023年07月14日 23:00 290
admin
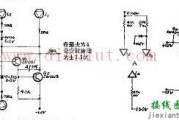
经典三运放仪表放大器
图 1 所示的三运放结构是一种常用的仪表放大器电路，可提供高 CMRR 以及平衡的高输入阻抗。
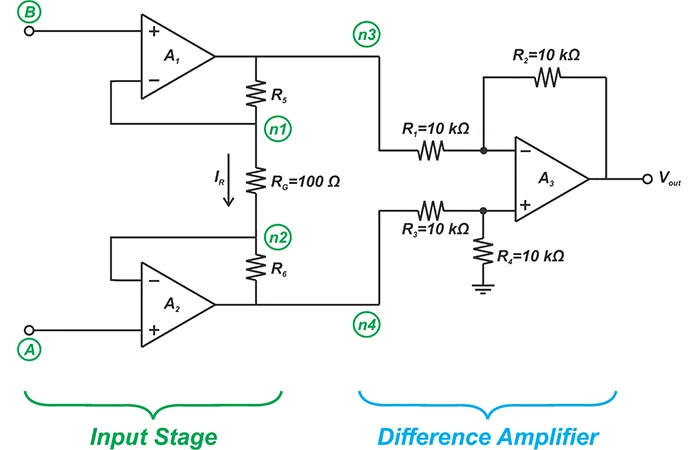上面的示意图可以分解为两部分。输入级主要充当缓冲器。输出级是前一篇文章中讨论过的差分放大器。正如我们将在下面看到的，三运放仪表放大器采用了巧妙的架构，具有一些有趣的功能。
高、平衡的输入阻抗
节点 A 和 B 都连接到相应运算放大器的非反相输入。这提供了高、平衡的输入阻抗，而无需诉诸复杂的反馈技术。
输入级可提供高差分增益和 CMRR
我们首先计算输入级的差分增益。负反馈以及运算放大器的高增益将迫使 A 1和 A 2的反相输入和同相输入具有相同的电压。因此，我们有：
\[v_{n1}=v_B\]
\[v_{n2}=v_A\]
通过 R G以及因此通过 R 5和 R 6 的电流将为：
\[I_R=\frac{v_{n1}-v_{n2}}{R_G}=\frac{v_B-v_A}{R_G}\]
因此，当R 5 =R 6时，差分放大器输入端的电压差将为：
\[v_{n3}-v_{n4}=(R_5+R_G+R_6) \times I_R=(2R_5+R_G) \times \frac{v_B-v_A}{R_G}\]
这简化为
\[v_{n3}-v_{n4}=\left ( \frac{2R_5}{R_G}+1 \right )\times (v_B-v_A)\]
公式1
我们知道差分放大器的增益为：
\[v_{out}=\frac{R_2}{R_1}(v_{n4}-v_{n3})\]
因此，我们有：
\[v_{out}=\frac{R_2}{R_1}\left ( \frac{2R_5}{R_G}+1 \right )\times (v_{A}-v_{B})\]
因此，电路的总差模增益为：
\[A_d=\frac{R_2}{R_1}\left ( \frac{2R_5}{R_G}+1 \right )\]
公式 1 显示输入级的差分增益 A d1可以通过选择 R 5和 R G的值进行调整。例如，对于图 1 中的典型值且 R 5 = 50 kΩ，A d1将为：
\[A_{d1}=\frac{v_{n3}-v_{n4}}{v_B-v_A}= \frac{2R_5}{R_G}+1=\frac{2 \times 50 k \Omega}{100 \欧米茄}+1=1001\]
公式2
输入级的共模增益是多少？根据以上分析，当v A =v B时，R G两端的电压将为零。因此，没有电流流过R 5、R G和R 6；我们有：
\[v_{n3}=v_{n4}=v_A=v_B\]
总而言之，输入级可以为我们提供较大的差分增益，同时以单位增益传递共模信号。这导致输入级的 CMRR 相对较高。接下来，差分放大器将进一步抑制该残余共模信号。输入级的一个有趣特性是增加差分增益也会增加 CMRR。
图 1 所示的三运放结构是一种常用的仪表放大器电路，可提供高 CMRR 以及平衡的高输入阻抗。
上面的示意图可以分解为两部分。输入级主要充当缓冲器。输出级是前一篇文章中讨论过的差分放大器。正如我们将在下面看到的，三运放仪表放大器采用了巧妙的架构，具有一些有趣的功能。高、平衡的输入阻抗
节点 A 和 B 都连接到相应运算放大器的非反相输入。这提供了高、平衡的输入阻抗，而无需诉诸复杂的反馈技术。
输入级可提供高差分增益和 CMRR
我们首先计算输入级的差分增益。负反馈以及运算放大器的高增益将迫使 A 1和 A 2的反相输入和同相输入具有相同的电压。因此，我们有：
\[v_{n1}=v_B\]
\[v_{n2}=v_A\]
通过 R G以及因此通过 R 5和 R 6 的电流将为：
\[I_R=\frac{v_{n1}-v_{n2}}{R_G}=\frac{v_B-v_A}{R_G}\]
因此，当R 5 =R 6时，差分放大器输入端的电压差将为：
\[v_{n3}-v_{n4}=(R_5+R_G+R_6) \times I_R=(2R_5+R_G) \times \frac{v_B-v_A}{R_G}\]
这简化为
\[v_{n3}-v_{n4}=\left ( \frac{2R_5}{R_G}+1 \right )\times (v_B-v_A)\]
公式1
我们知道差分放大器的增益为：
\[v_{out}=\frac{R_2}{R_1}(v_{n4}-v_{n3})\]
因此，我们有：
\[v_{out}=\frac{R_2}{R_1}\left ( \frac{2R_5}{R_G}+1 \right )\times (v_{A}-v_{B})\]
因此，电路的总差模增益为：
\[A_d=\frac{R_2}{R_1}\left ( \frac{2R_5}{R_G}+1 \right )\]
公式 1 显示输入级的差分增益 A d1可以通过选择 R 5和 R G的值进行调整。例如，对于图 1 中的典型值且 R 5 = 50 kΩ，A d1将为：
\[A_{d1}=\frac{v_{n3}-v_{n4}}{v_B-v_A}= \frac{2R_5}{R_G}+1=\frac{2 \times 50 k \Omega}{100 \欧米茄}+1=1001\]
公式2
输入级的共模增益是多少？根据以上分析，当v A =v B时，R G两端的电压将为零。因此，没有电流流过R 5、R G和R 6；我们有：
\[v_{n3}=v_{n4}=v_A=v_B\]
总而言之，输入级可以为我们提供较大的差分增益，同时以单位增益传递共模信号。这导致输入级的 CMRR 相对较高。接下来，差分放大器将进一步抑制该残余共模信号。输入级的一个有趣特性是增加差分增益也会增加 CMRR。
相关文章
发表评论